

An equation containing a second-degree polynomial is called a quadratic equation. The standard form of a quadratic equation is \(ax^2 +bx+c=0\) where \(a\) is called the leading coefficient. For example, equations such as \(2x^2 +3x−1=0\) and \(x^2−4= 0\) are quadratic equations. They are used in countless ways in the fields of engineering, architecture, finance, biological science, and, of course, mathematics.
Factor and solve the quadratic equation: \(x^2−5x−6=0\).
Solve the quadratic equation by factoring: \(x^2+8x+15=0\).
Solution
Find two numbers whose product equals \(15\) and whose sum equals \(8\). List the factors of \(15\).
The numbers that add to \(8\) are \(3\) and \(5\). Then, write the factors, set each factor equal to zero, and solve.
The solutions are \(−3\) and \(−5\).
Solve the quadratic equation by factoring: \(x^2−4x−21=0\).
Solve the difference of squares equation using the zero-product property: \(x^2−9=0\).
Solution
Recognizing that the equation represents the difference of squares, we can write the two factors by taking the square root of each term, using a minus sign as the operator in one factor and a plus sign as the operator in the other. Solve using the zero-factor property.
The solutions are \(3\) and \(−3\).
Solve by factoring: \(x^2−25=0\).
When the leading coefficient is not \(1\), we factor a quadratic equation using the method called grouping, which requires four terms.
With the equation in standard form, let’s review the grouping procedures
Use grouping to factor and solve the quadratic equation: \(4x^2+15x+9=0\).
Solution
First, multiply \(ac:4(9)=36\). Then list the factors of \(36\).
The only pair of factors that sums to \(15\) is \(3+12\). Rewrite the equation replacing the b term, \(15x\), with two terms using \(3\) and \(12\) as coefficients of \(x\). Factor the first two terms, and then factor the last two terms.
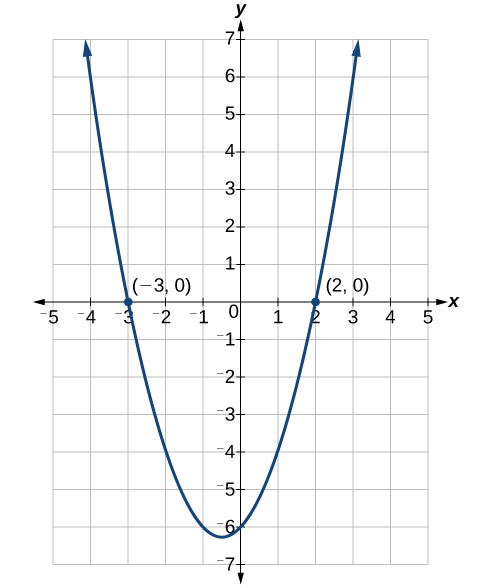
The solutions are \(−\dfrac\), and \(−3\). See Figure \(\PageIndex\).
Solve using factoring by grouping: \(12x^2+11x+2=0\).
Solve the equation by factoring: \(−3x^3−5x^2−2x=0\).
Solution
This equation does not look like a quadratic, as the highest power is \(3\), not \(2\). Recall that the first thing we want to do when solving any equation is to factor out the GCF, if one exists. And it does here. We can factor out \(−x\) from all of the terms and then proceed with grouping.
The solutions are \(0\), \(−\dfrac\), and \(−1\).
Solve by factoring: \(x^3+11x^2+10x=0\).
When there is no linear term in the equation, another method of solving a quadratic equation is by using the square root property, in which we isolate the \(x^2\) term and take the square root of the number on the other side of the equals sign. Keep in mind that sometimes we may have to manipulate the equation to isolate the \(x^2\) term so that the square root property can be used.
With the \(x^2\) term isolated, the square root property states that:
if \(x^2=k\), then \(x=±\sqrtwhere \(k\) is a nonzero real number.
Solve the quadratic using the square root property: \(x^2=8\).
Solution
Take the square root of both sides, and then simplify the radical. Remember to use a \(±\) sign before the radical symbol.
The solutions are \(2\sqrt\),\(-2\sqrt\)
Solve the quadratic equation: \(4x^2+1=7\).
Solution
First, isolate the \(x^2\) term. Then take the square root of both sides.
Solve the quadratic equation using the square root property: \(3^2=15\).
Not all quadratic equations can be factored or can be solved in their original form using the square root property. In these cases, we may use a method for solving a quadratic equation known as completing the square. Using this method, we add or subtract terms to both sides of the equation until we have a perfect square trinomial on one side of the equal sign. We then apply the square root property. To complete the square, the leading coefficient, \(a\), must equal \(1\). If it does not, then divide the entire equation by \(a\). Then, we can use the following procedures to solve a quadratic equation by completing the square.
We will use the example \(x^2+4x+1=0\) to illustrate each step.
Given a quadratic equation that cannot be factored, and with \(a=1\), first add or subtract the constant term to the right sign of the equal sign.
The solutions are \(−2+\sqrt\), and \(−2−\sqrt\).
Solve the quadratic equation by completing the square: \(x^2−3x−5=0\).
Solution
First, move the constant term to the right side of the equal sign.